
Astoro Compute
 |
もしも月面に立つと地平線としてどのくらいの距離を見渡せるのでしょうか? |
地平線は遙か彼方という印象が在りますが、球体の星の上では見渡せる範囲は意外にも狭いものです。
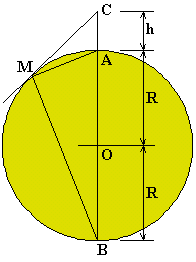 |
左の図で、目の位置をC、目の位置から月表面に引いた接線をCMとすれば、CMが地平線までの距離となります。 Cと月の中心Oを結ぶ直線が月表面と交わる点をA,Bとすると
hは2R(月の直径)に比べて非常に小さいとすればh/2Rは無視できますので
|
それぞれに実際の数値を代入して計算してみましょう。
月面に立つ人の目の高さを1.5mとします。
h=1.5m=1.5×10-3km
月半径R=1738.092km
月の地平線までの距離は
|
=√2Rh |
=√2×1738.092×1.5×10-3 |
=√5.214576 |
|
=2.2835kmとなります。 | ||
意外にも小さいと思われるかも知れません。
その昔、月は平らな板のように思われていたことを考えると、何と小さくなってしまうことでしょう。
それでは直径が3.6倍も大きな地球ではどうでしょうか?
上記の計算式でRが6371.012kmとなるだけで計算できます。
|
=√2Rh |
=√2×6371.012×1.5×10-3 |
=√19.11303 |
|
=4.3718kmとなります。 | ||
ただし地球には大気があり、屈折による影響が無視できません。
これは大気差と言われるもので約6%程遠くまで見えることになりますので
4.3718×1.06としても4.634kmに過ぎません。
|
見渡せる範囲は円形になりますので、その面積はπr |
2 |
で求めると |
|
|
|
37.462km |
2 |
しかありません。 |
|
|
これを四角形で表すと8.21km四方と言うことになります。
hを人の目の高さとしましたが、高層ビルからや富士山頂などとして計算してみるとかなり広がることが分かります。
遠くを見張る火の見櫓が高さを競うように天高くそびえるのは、それだけ遠くを見るために有効な方法であることが分かります。
