
MOON FAQ
このページでは、皆さんから戴いたご質問にお応えするページです。
メールによる文字だけの説明では、分かりにくいことなどをHTMLページでお伝えいています。
月は地球の周りを回っています。
その軌道は完全な円では無く、楕円軌道と呼ばれるものです。
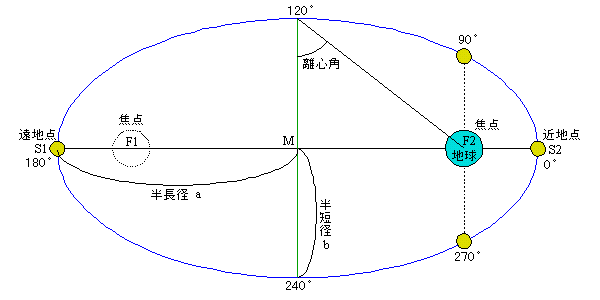
実際の軌道を極端に誇張した図です。
楕円軌道の中心点Mの地点に地球があると思われている方も多いようですが、
楕円軌道の焦点は2つありその内一方の焦点上に地球は位置しています。
こうして地球の周りを回る月は、近地点から遠地点へ、そしてまた近地点へと戻ってきます。
こうして月が地球の周りを回る楕円軌道は常にほぼ一定の方向を向いていますので、
太陽の周りを地球が公転して行くことで太陽の方向だけが変わって行くように感じられます。
厳密には月の公転軌道(白道)は一定の方向ではなく、
約18年という長い時間を掛けてその向きが回転しています。
地球が公転することによって太陽の方向が変わってくるために、
同じ満月でも遠地点の時もあれば近地点の時も起こることになります。
例えば、近地点S2に月がいるとしましょう。
その時太陽が180度の方向にあるとすれば、その時近地点を迎えた満月となります。
逆に、遠地点S1に月がいる場合に、太陽が0度方向であった場合には、
同じく満月ですが遠地点の満月と言うことになります。
毎日見る月も、その時の軌道上の位置によって、地球からの距離が違います。
約27日周期で+−2万キロも変化しています。
月の見掛けの直径は角度にして平均31分5.2秒ですが、
最大33分47.4秒から最小29分22.9秒の間で変化します。
見掛けの大きさの違いは地球からの距離変化により周期的に変化しています。
この変化によって、日食が皆既や金環食となったりします。
実際に撮らえた画像で確認してみましょう。
 |  |
|
|
1998/03/13 405,500kmの満月 |
1999/01/03 369,600kmの満月 |
|
同じ倍率で同じ画像サイズのものです。(画像:今日の月より) |
||
それぞれ満月において最も遠い時と近づいた時のものです。
市販のデジタルカメラで撮えたものですので、画質は良くありませんが、
充分に大きさの違いが分かって戴けるものと思います。
そこで、昨年1年間の月距離変化をグラフにしてみました。
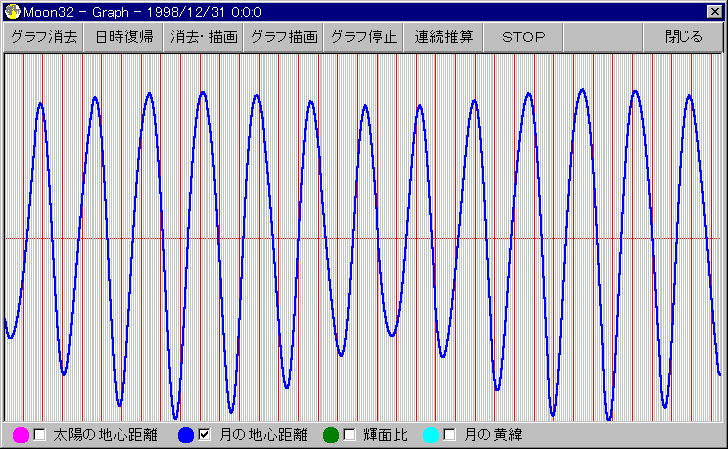
グラフ作成 Moon32 Ver2.21c(横軸は365日分:縦赤線は10日毎)
月と地球の平均距離は384,401kmですが、平均で27日と13時間18分の周期で遠近を繰り返しています。
しかし地心距離の変化を見て行くと、最遠距離や最近距離が変化していることに気が付きます。
遠地点での距離変化に比べて近地点での変化が大きいことも分かると思います。
どうして同じ楕円軌道上を進む月の最遠・最近距離が変化してしまうのでしょう?
惑星や彗星を含め、月もまた太陽引力との相互作用によって運動しています。
単純に地球と月だけの2つの天体だけであれば、
ニュートンやケプラーの運動法則によって、完全に運動状態が決まります。
しかし他の天体の重力的影響が無視できないときには、その運動は乱されてしまいます。
これを「摂動」と言い、その軌道要素は少しずつ変化して行くことになります。
摂動には惑星間の会合周期と同じ周期を持つ「周期摂動」と、
次第に累積していく「永年摂動」がありますが、
特に月を始め彗星・小惑星の位置予報などでは、この摂動計算が必要になります。
月の位置推算が最も難しいことの要因はこの「摂動」にあるのです。
1998年においては最遠距離 406,667km(10/21)、最近距離は 356,611km(11/04)まで変化しています。
