
Astoro Compute
 |
地球にはたらく太陽と月の引力の比率はどのくらいなのでしょうか? |
まず、地球にはたらく力について考えてみましょう。
地球にはたらく力には万有引力と遠心力があります。
はじめに地球の中心にはたらく、月の遠心力と万有引力を計算してみましょう。
|
共通重心 地球の質量 月の質量 月の地心距離 月の公転周期 万有引力定数 |
W M m a P G |
は 4.72759x108 cm は 5.974x1027 g は 7.3471x1025 g は 3.84401x1010 cm は 2.361x106 秒(1恒星月) は 6.672x10-8 cm/g/秒2 |
となります。 |
地心に於ける重さ1gに対する月の万有引力Fは以下の式が成り立ちます。
|
F M |
= |
Gm a2 |
= |
6.672x10-8 × 7.3471x1025 3.84401x1010 × 3.84401x1010 |
|
F M |
= |
3.317439x10-3 cm/秒2 |
次に地球が月との共通重心を回る遠心力を計算してみましょう。
重さ1gに対する地球の遠心力Cは次の式で求めます。
|
C= |
( |
2πW P |
) |
2 |
1 W |
|
|
|
C= |
( |
2π4.72759x108 2.361x106 |
) |
2 |
1 4.72759x108 |
|
|
C=3.348167x10-3 cm/秒2
以上の結果から
|
C≒ |
F M |
地球の中心では万有引力と遠心力が、ほぼ等しいと言えます。
以上のことを前提として、月と太陽の万有引力と遠心力を地球表面2点について計算してみます。
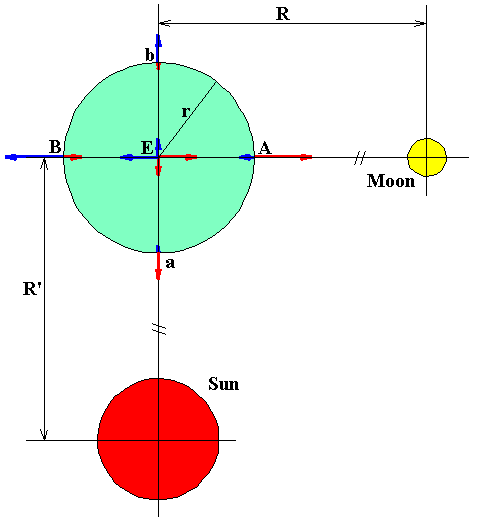
上の図で、Eを地心、A,Bは月に面した点と正反対の点です。 同様にa,bは太陽に面した点と正反対の面です。
A点の合成値は(万有引力)−(遠心力)ですので、 =1.12760914x10-4 cm/秒2 となります。
B点の合成値は(遠心力)−(万有引力)ですので、 =1.07290765x10-4 cm/秒2 となります。 A・B点における合成値はほぼ等しと言えます。 同様にmを太陽の質量Sに、Rを太陽の地心距離をR’に それぞれ置き換えて計算すると
a点の合成値は(万有引力)−(遠心力)ですので、 =5.03764x10-5 cm/秒2 となります。
b点の合成値は(遠心力)−(万有引力)ですので、 =5.0505x10-5 cm/秒2 となります。 a・b点における合成値はほぼ等しと言えます。 |
A・aとB・bそれぞれの地点の合成値の比率を計算すると月と太陽が及ぼす引力の比率を求めることが出来ます
|
太陽の巨大な質量は強力な引力を及ぼしますがが、月に比べ大変遠方にあるために
結果的には月の引力が約2.2倍もの作用を及ぼすことになります。
この合成値とは、言い換えると起潮力のことを指します。
地球・月・太陽が直線に並んだときには、月と太陽の起潮力が一致し最大となります。
満月や新月の時には起潮力が最大となり大潮となります。
また、月と太陽が90度の角度になったときには、月と太陽の起潮力は分散し最小となります。
上弦や下弦の月の時には起潮力が最小となり小潮となります。

